Законы Кеплера
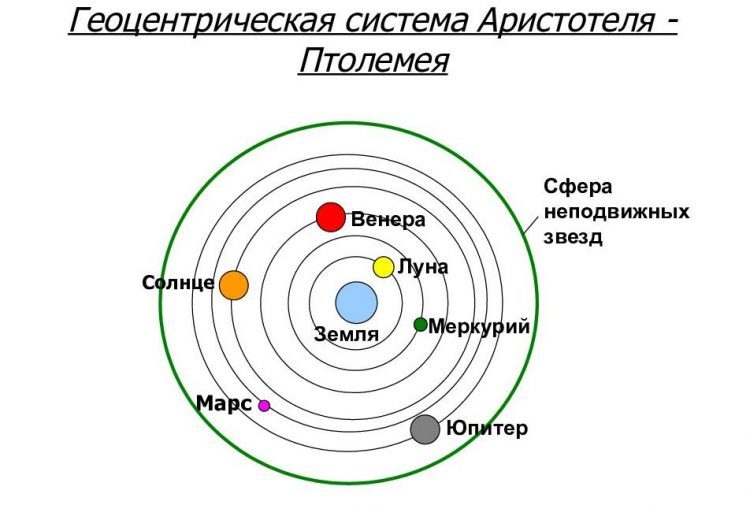
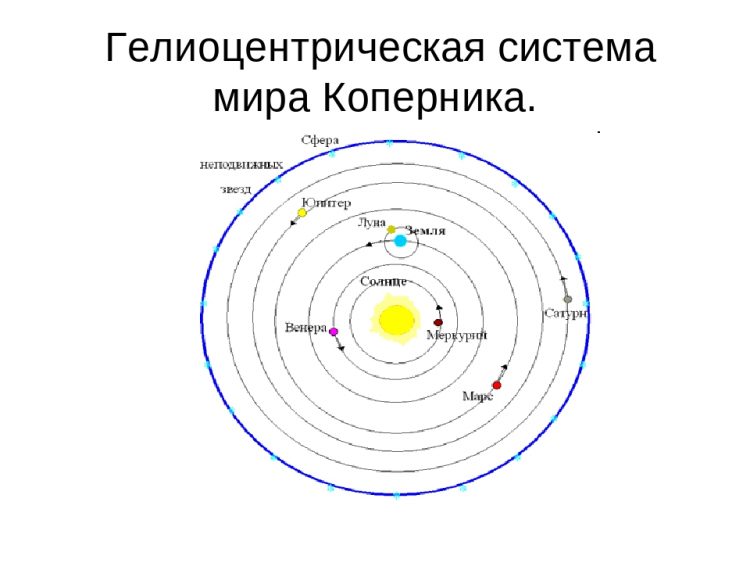
На рубеже XVI и XVII веков астрономия стояла на перепутье. Долгое время господствовала геоцентрическая система Птолемея, в которой все небесные тела вращались вокруг Земли. Однако уже после появления гелиоцентрической модели Коперника стало ясно, что Солнце играет центральную роль в движении планет. Проблема заключалась в том, что Коперник считал орбиты круговыми, что не соответствовало точным астрономическим наблюдениям.
Именно поэтому потребовались новые подходы для объяснения движения планет. Ими занялся немецкий учёный Иоганн Кеплер, изучая данные датского астронома Тихо Браге, который собрал огромное количество высокоточных измерений положения планет, особенно Марса.
Первый закон Кеплера (Закон эллипсов)
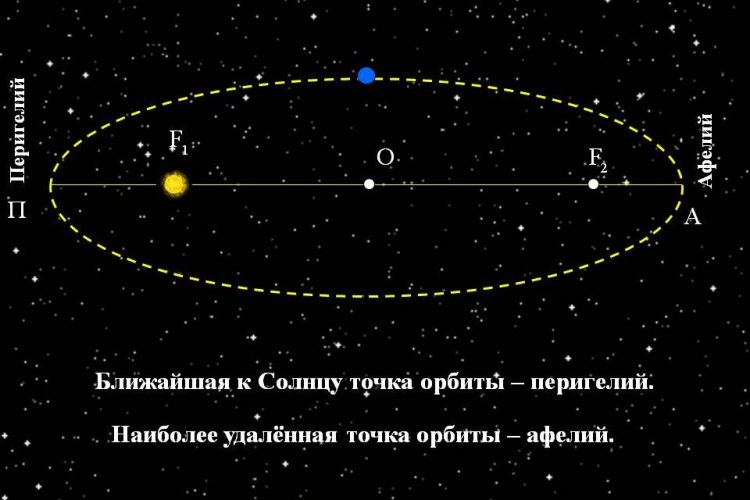
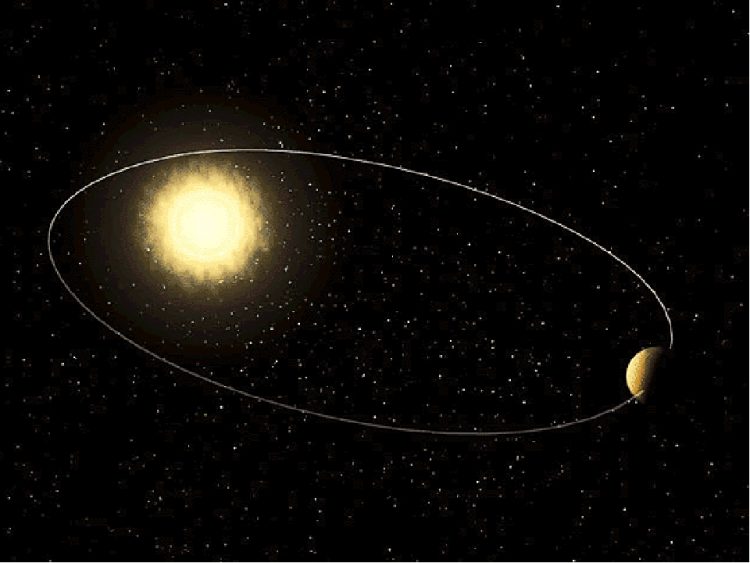
Кеплер установил, что планеты движутся не по окружностям, как предполагал Коперник, а по эллиптическим орбитам, и Солнце находится не в центре, а в одном из фокусов этой кривой.
Основная идея:
Все планеты Солнечной системы обращаются вокруг Солнца по эллипсам, один из фокусов которых совпадает с положением Солнца.
Это был революционный шаг — впервые движение планет описывалось математически точно, без сложных эпициклов и деферентов, которые использовались ранее.
- Эллипс — это геометрическая фигура, у которой сумма расстояний от любой точки на кривой до двух фокусов остаётся постоянной.
- У некоторых планет, таких как Венера и Нептун, орбита почти круговая.
- Самые заметные отклонения от круга наблюдаются у Марса и Плутона, если его всё ещё считать планетой.
Этот закон позволил более точно определять положение планет на небе и стал основой для последующих открытий.
Второй закон Кеплера (Закон площадей)
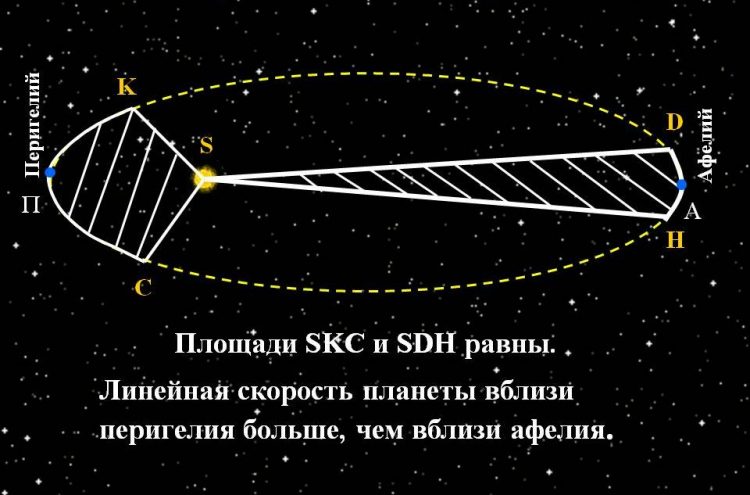
Если первый закон разрушил миф о круговых орбитах, то второй показал, что движение планет неравномерно. Чем ближе планета к Солнцу, тем быстрее она движется.
Формулировка второго закона:
Радиус-вектор планеты за равные промежутки времени описывает равные площади.
Это значит, что если провести воображаемую линию от Солнца к планете, то скорость её «заметания» площади будет постоянной.
Что это даёт?
- Когда планета находится в перигелии (ближайшая к Солнцу точка), она движется быстрее.
- В афелии (самая удалённая точка) — медленнее.
- Например, Земля в январе проходит перигелий и движется чуть быстрее, чем летом, когда она находится в афелии.
Этот принцип можно применять не только к планетам, но и к спутникам, кометам и другим объектам, обращающимся вокруг звезд или планет.
Третий закон Кеплера (Гармонический закон)
Третий закон связывает время обращения планеты вокруг Солнца с её средним расстоянием до него. Это было важнейшее обобщение, позволившее вычислять параметры орбит даже теоретически.
Формулировка:
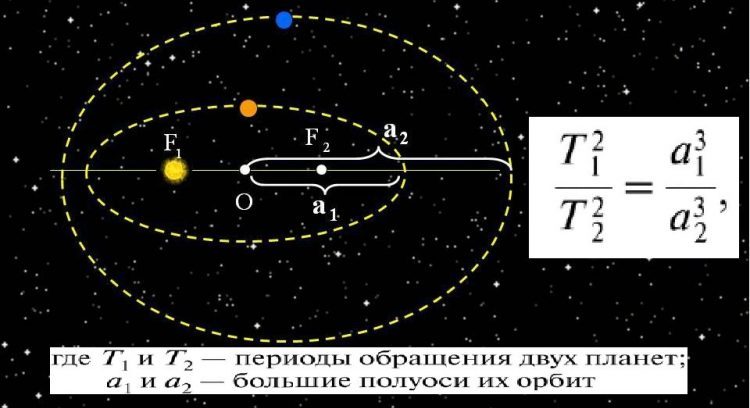
Квадраты периодов обращения планет относятся между собой как кубы их средних расстояний до Солнца.
Математически это выражается так:
T₁² / T₂² = a₁³ / a₂³,
где T — период обращения, a — большая полуось орбиты.
Практическое значение:
- Можно рассчитать расстояние до планет, зная их период обращения;
- На основе этого закона позже были определены массы других светил;
- Он стал ключевым при изучении спутников Юпитера и Сатурна, а также экзопланет, обращающихся вокруг далёких звёзд.
Третий закон помог понять, почему внутренние планеты движутся быстро, а внешние — медленно. Например, Меркурий делает полный оборот за 88 дней, тогда как Нептун — за 165 лет.
Как Кеплер пришёл к этим законам?
Ключевую роль сыграло сотрудничество Кеплера с Тихо Браге. Последний собирал очень точные данные о положении планет, особенно о Марсе, в течение многих лет. После его смерти Кеплер получил доступ к этим данным и начал их анализировать.
Он потратил десять лет, чтобы понять, что орбита Марса — не круг, а эллипс. Эта работа стала основой первого закона. Затем он обобщил свои выводы на другие планеты и сформулировал второй и третий законы.
Без этих данных и долгих вычислений невозможно было бы создать новую модель движения планет, которая заменила собой древнюю систему Птолемея.
Значение законов Кеплера
Эти три закона стали поворотным моментом в астрономии:
- Они полностью разрушили представление о круговых орбитах.
- Объяснили видимое неравномерное движение планет на небе.
- Легли в основу ньютоновской теории гравитации, поскольку Ньютон использовал их для вывода своего закона всемирного тяготения.
- Служат базой для космической механики, необходимой для запуска спутников и межпланетных станций.
Современные применения
Сегодня законы Кеплера применяются в различных областях:
- При расчёте орбит искусственных спутников.
- Для прогнозирования движения астероидов и комет.
- При изучении экзопланет и двойных звёзд.
- В расчётах траекторий марсоходов и зондов.
Они позволяют определить, например, когда Юпитер будет находиться в противостоянии, или какова должна быть траектория корабля, отправляющегося к Марсу.
Интересные факты
- Первый закон означает, что ни одна планета не движется строго по окружности, хотя у Венеры орбита наиболее близка к круговой.
- Второй закон объясняет, почему Земля движется быстрее зимой, чем летом.
- Третий закон используется в поиске планет вне Солнечной системы, где достаточно знать период обращения, чтобы вычислить расстояние до звезды.
- Эти законы справедливы не только для планет, но и для спутников, звёздных систем и даже галактик.
- Именно благодаря им мы знаем, что Солнечная система обращается вокруг центра Галактики, и один такой оборот занимает около 200 миллионов лет.
Похожие статьи

На рубеже XVI и XVII веков астрономия стояла на перепутье. Долгое время господствовала геоцентрическая система Птолемея, в которой все небесные тела вращались вокруг Земли. Однако уже после появления гелиоцентрической модели Коперника стало ясно, что Солнце играет центральную роль в движении планет. Проблема заключалась в том, что Коперник считал орбиты круговыми, что не соответствовало точным астрономическим наблюдениям.
Именно поэтому потребовались новые подходы для объяснения движения планет. Ими занялся немецкий учёный Иоганн Кеплер, изучая данные датского астронома Тихо Браге, который собрал огромное количество высокоточных измерений положения планет, особенно Марса.
Первый закон Кеплера (Закон эллипсов)

Кеплер установил, что планеты движутся не по окружностям, как предполагал Коперник, а по эллиптическим орбитам, и Солнце находится не в центре, а в одном из фокусов этой кривой.
Основная идея:
Все планеты Солнечной системы обращаются вокруг Солнца по эллипсам, один из фокусов которых совпадает с положением Солнца.
Это был революционный шаг — впервые движение планет описывалось математически точно, без сложных эпициклов и деферентов, которые использовались ранее.

- Эллипс — это геометрическая фигура, у которой сумма расстояний от любой точки на кривой до двух фокусов остаётся постоянной.
- У некоторых планет, таких как Венера и Нептун, орбита почти круговая.
- Самые заметные отклонения от круга наблюдаются у Марса и Плутона, если его всё ещё считать планетой.
Этот закон позволил более точно определять положение планет на небе и стал основой для последующих открытий.

Второй закон Кеплера (Закон площадей)

Если первый закон разрушил миф о круговых орбитах, то второй показал, что движение планет неравномерно. Чем ближе планета к Солнцу, тем быстрее она движется.
Формулировка второго закона:
Радиус-вектор планеты за равные промежутки времени описывает равные площади.
Это значит, что если провести воображаемую линию от Солнца к планете, то скорость её «заметания» площади будет постоянной.
Что это даёт?
- Когда планета находится в перигелии (ближайшая к Солнцу точка), она движется быстрее.
- В афелии (самая удалённая точка) — медленнее.
- Например, Земля в январе проходит перигелий и движется чуть быстрее, чем летом, когда она находится в афелии.
Этот принцип можно применять не только к планетам, но и к спутникам, кометам и другим объектам, обращающимся вокруг звезд или планет.
Третий закон Кеплера (Гармонический закон)

Третий закон связывает время обращения планеты вокруг Солнца с её средним расстоянием до него. Это было важнейшее обобщение, позволившее вычислять параметры орбит даже теоретически.
Формулировка:
Квадраты периодов обращения планет относятся между собой как кубы их средних расстояний до Солнца.
Математически это выражается так:
T₁² / T₂² = a₁³ / a₂³,
где T — период обращения, a — большая полуось орбиты.
Практическое значение:
- Можно рассчитать расстояние до планет, зная их период обращения;
- На основе этого закона позже были определены массы других светил;
- Он стал ключевым при изучении спутников Юпитера и Сатурна, а также экзопланет, обращающихся вокруг далёких звёзд.
Третий закон помог понять, почему внутренние планеты движутся быстро, а внешние — медленно. Например, Меркурий делает полный оборот за 88 дней, тогда как Нептун — за 165 лет.
Как Кеплер пришёл к этим законам?
Ключевую роль сыграло сотрудничество Кеплера с Тихо Браге. Последний собирал очень точные данные о положении планет, особенно о Марсе, в течение многих лет. После его смерти Кеплер получил доступ к этим данным и начал их анализировать.
Он потратил десять лет, чтобы понять, что орбита Марса — не круг, а эллипс. Эта работа стала основой первого закона. Затем он обобщил свои выводы на другие планеты и сформулировал второй и третий законы.
Без этих данных и долгих вычислений невозможно было бы создать новую модель движения планет, которая заменила собой древнюю систему Птолемея.
Значение законов Кеплера
Эти три закона стали поворотным моментом в астрономии:
- Они полностью разрушили представление о круговых орбитах.
- Объяснили видимое неравномерное движение планет на небе.
- Легли в основу ньютоновской теории гравитации, поскольку Ньютон использовал их для вывода своего закона всемирного тяготения.
- Служат базой для космической механики, необходимой для запуска спутников и межпланетных станций.
Современные применения
Сегодня законы Кеплера применяются в различных областях:
- При расчёте орбит искусственных спутников.
- Для прогнозирования движения астероидов и комет.
- При изучении экзопланет и двойных звёзд.
- В расчётах траекторий марсоходов и зондов.
Они позволяют определить, например, когда Юпитер будет находиться в противостоянии, или какова должна быть траектория корабля, отправляющегося к Марсу.
Интересные факты
- Первый закон означает, что ни одна планета не движется строго по окружности, хотя у Венеры орбита наиболее близка к круговой.
- Второй закон объясняет, почему Земля движется быстрее зимой, чем летом.
- Третий закон используется в поиске планет вне Солнечной системы, где достаточно знать период обращения, чтобы вычислить расстояние до звезды.
- Эти законы справедливы не только для планет, но и для спутников, звёздных систем и даже галактик.
- Именно благодаря им мы знаем, что Солнечная система обращается вокруг центра Галактики, и один такой оборот занимает около 200 миллионов лет.